数据结构and数据建模and数据算法
常见数据结构及原理
数据结构
1.线性表
线性表是最常用且最简单的一种数据结构,它是n个数据元素的有限序列。 实现方式:
1.数组:大小固定,满了需要用更大数组替换;查找快,插入、删除慢(需要移动后面数据位置)
2.链表:通过链表中的指针链接次序实现;插入、删除快,查找慢
单链表反转:https://blog.csdn.net/blioo/article/details/62050967
2.栈与队列
栈和队列也是比较常见的数据结构,它们是比较特殊的线性表,因为对于栈来说,访问、插入和删除元素只能在栈顶进行(后进先出);对于队列来说,元素只能从队列尾插入,从队列头访问和删除(先进先出)。
1.栈:栈是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫作栈顶;
对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者相当于删除最后一个元素。
栈有时又叫作LIFO(Last In First Out)表,即后进先出。
2.队列:队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作;
而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。
进行插入操作的端称为队尾,进行删除操作的端称为队头。
3.树与二叉树
1.树(Tree)是一个分层的数据结构,由节点和连接节点的边组成;
2.二叉树与树的主要区别:前者必须区分左右子树(即使只有一棵子树)
3.平衡二叉树(AVL),所有节点的左右子树深度都不超过1(只有左子树的树其实就是链表)
查找、插入和删除在平均和最坏情况下都是O(logn)
追求绝对平衡,不平衡需要旋转(耗时),所以插入删除慢,纯查找快;
4.jdk1.8后,java对HashMap做了改进,在链表长度大于8的时候,将后面的数据存在红黑树中,以加快检索速度
5.红黑树,查找、插入、删除时间复杂度都是O(logn)
追求大致平衡,保证每次插入最多只需要三次旋转就能达到平衡
查找时间复杂度与AVL相同,但是插入,删除快;
原文:https://baijiahao.baidu.com/s?id=1609911567564476905&wfr=spider&for=pc
数据建模
3NF(三范式)
第一范式:字段具有原子性,不可再分;
第二范式:满足第一范式的基础上,要求数据库表中的每个实例或行必须可以被唯一地区分;
第三范式:满足第二范式的基础上,数据库表中不包含已在其它表中已包含的非主关键字信息。
简单说:
1,每一列只有一个值
2,每一行都能区分
3,每一个表都不包含其他表已经包含的非主关键字信息。
数据模型三要素
1.数据结构
2.数据操作
3.完整性约束
三种最常用数据模型
1.层次模型
层次模型将数据组织成一对多关系的结构,层次结构采用关键字来访问其中每一层次的每一部分。
以树结构为基本结构,典型代表是IMS模型。
优点是存取方便且速度快;结构清晰,容易理解;数据修改和数据库扩展易实现;检索关键属性方便。
2.网状模型
网状模型用连接指令或指针来确定数据间的显式连接关系,是具有多对多类型的数据组织方式。
目前使用仍较多,典型代表是DBTG模型。
优点是能明确而方便地表示数据间的复杂关系。
3.关系模型
关系模型以记录组或数据表的形式组织数据,以便于利用各种地理实体与属性之间的关系进行存储和变换,
不分层也无指针,是建立空间数据和属性数据之间关系的一种非常有效的数据组织方法。
优点在于结构特别灵活,概念单一,满足所有布尔逻辑运算和数学运算规则形成的查询要求;
能搜索、组合和比较不同类型的数据;增加和删除数据非常方便。
其它常见数据模型
1.星型模型
数据集市维度建模中推荐的方法。
以事实表为中心,所有的维度表直接连接在事实表上,像星星一样。(维度表不能有子维度表)
2.雪花模型
维度表可以拥有其他维度表
维护成本比较高,而且性能方面需要关联多层维表,性能也比星型模型要低。一般不是很常用。
3.范式建模
第三范式建模是在数据库建模中使用的建模方法
体系化,扩展性好,避免冗余,避免更新异常。
按层级分类
1.概念模型
面向客观世界、面向用户,与具体的数据库管理系统无关,与具体的计算机平台无关。
2.逻辑模型
面向数据库系统的模型,
只有在转换成逻辑型之后才数据库中得以表示。
目前,逻辑模型的种类很多,其中比较成熟的包括层次模型、关系模型、网状模型、面向对象模型等。
3.物理模型
面向计算机物理表示的模型。此模型是数据模型在计算机物理结构上的表示。
这篇把概念写的比较详细,而且也有具体建模方法,优秀:
数据算法
1.二分法:
时间复杂度log(n)
/**
* @param args
*/
public static void main(String[] args) {
int[] arr = new int[] { 12, 23, 34, 45, 56, 67, 77, 89, 90 };
System.out.println(search(arr, 12));
System.out.println(search(arr, 45));
System.out.println(search(arr, 67));
System.out.println(search(arr, 89));
System.out.println(search(arr, 99));
}
public static int search(int[] arr, int key) {
int start = 0;
int end = arr.length - 1;
while (start <= end) {
int middle = (start + end) / 2;
if (key < arr[middle]) {
end = middle - 1;
} else if (key > arr[middle]) {
start = middle + 1;
} else {
return middle;
}
}
return -1;
}
2.快速排序
时间复杂度 O(NlogN)
public static void main(String[] args) {
int[] a = {11, 2, 4, 5, 7, 4, 5 ,3 ,9 ,0};
System.out.println(Arrays.toString(a));
quickSort(a);
System.out.println(Arrays.toString(a));
}
public static void quickSort(int[] a) {
if(a.length>0) {
quickSort(a, 0 , a.length-1);
}
}
private static void quickSort(int[] a, int low, int high) {
//1,找到递归算法的出口
if( low > high) {
return;
}
//2, 存
int i = low;
int j = high;
//3,key
int key = a[ low ];
//4,完成一趟排序
while( i< j) {
//4.1 ,从右往左找到第一个小于key的数
while(i<j && a[j] > key){
j--;
}
// 4.2 从左往右找到第一个大于key的数
while( i<j && a[i] <= key) {
i++;
}
//4.3 交换
if(i<j) {
int p = a[i];
a[i] = a[j];
a[j] = p;
}
}
// 4.4,调整key的位置
int p = a[i];
a[i] = a[low];
a[low] = p;
//5, 对key左边的数快排
quickSort(a, low, i-1 );
//6, 对key右边的数快排
quickSort(a, i+1, high);
}
3.hashmap累加:
if(map.containsKey(key1)){
map.put(key1,map.get(key1)+1);
}else{
map.put(key1,1);
}
4.hash均摊:
hash(key)%10 (均匀分为十份)
各种排序复杂度:
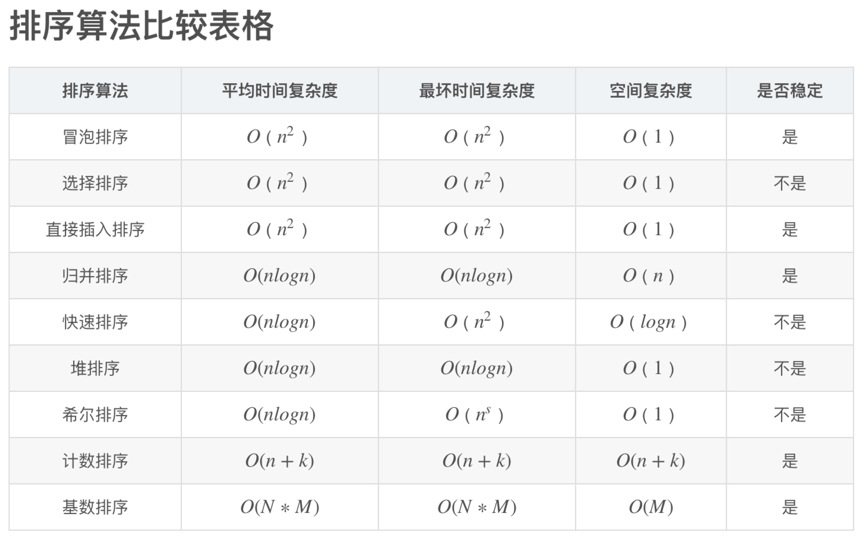
经典Demo
1.100G文件,在100M内存中的排序
方法1(经典,归并排序的思想):
100G 数据,按照 100M 内存拆分,然后排序有序的数据,然后写入到 file1,file2…fileN;
再多路归并;
步骤:
1.从 file1,file2……fileN,取出第一个数(已排序),即最小的。所有的初始指针都是第一行;
2.从这N个数中取出最小的(假定该数据在fileM中),放入结果文件中;
3.fileM指针指向第二行数据,其他文件还是指向第一行,N个数中选出最小的,放入结果文件中;
4.以此类推,最终全部按照顺序放入结果文件中,完成排序;
方法2(自创,有BUG):
如果数据连续且均匀。
1.先遍历出max,min,然后拆分出(max-min)/(100G/100M)的文件数,且排序文件名;
2.启动多个线程(理论最大为100M能放下的数据条数),分别将数据放入对应范文的文件内;
参考: https://www.cnblogs.com/benchen/p/6011721.html https://zhidao.baidu.com/question/7869959.html https://blog.csdn.net/clevercode/article/details/81743736