马太函数 and IV算法

最近工作中有接触到通过马太函数和iv算法进行特征筛选，虽然只是帮忙做一些简单的数据采集工作，不过，学习一下总归是多多益善的。

马太函数

马太效应，是指好的愈好，坏的愈坏，多的愈多，少的愈少的一种现象。即两极分化现象。

类似于80/20法则，它们大概说的意思是一致的，在统计学中，这些说法被抽象成所谓的幂律分布，在分布图上，它表现为一条拖着长长尾巴的曲线。

打个比方，我们取一个区域内拥有的财富为宗轴，拥有这些财富的人口为横轴，样本分布可能如下：

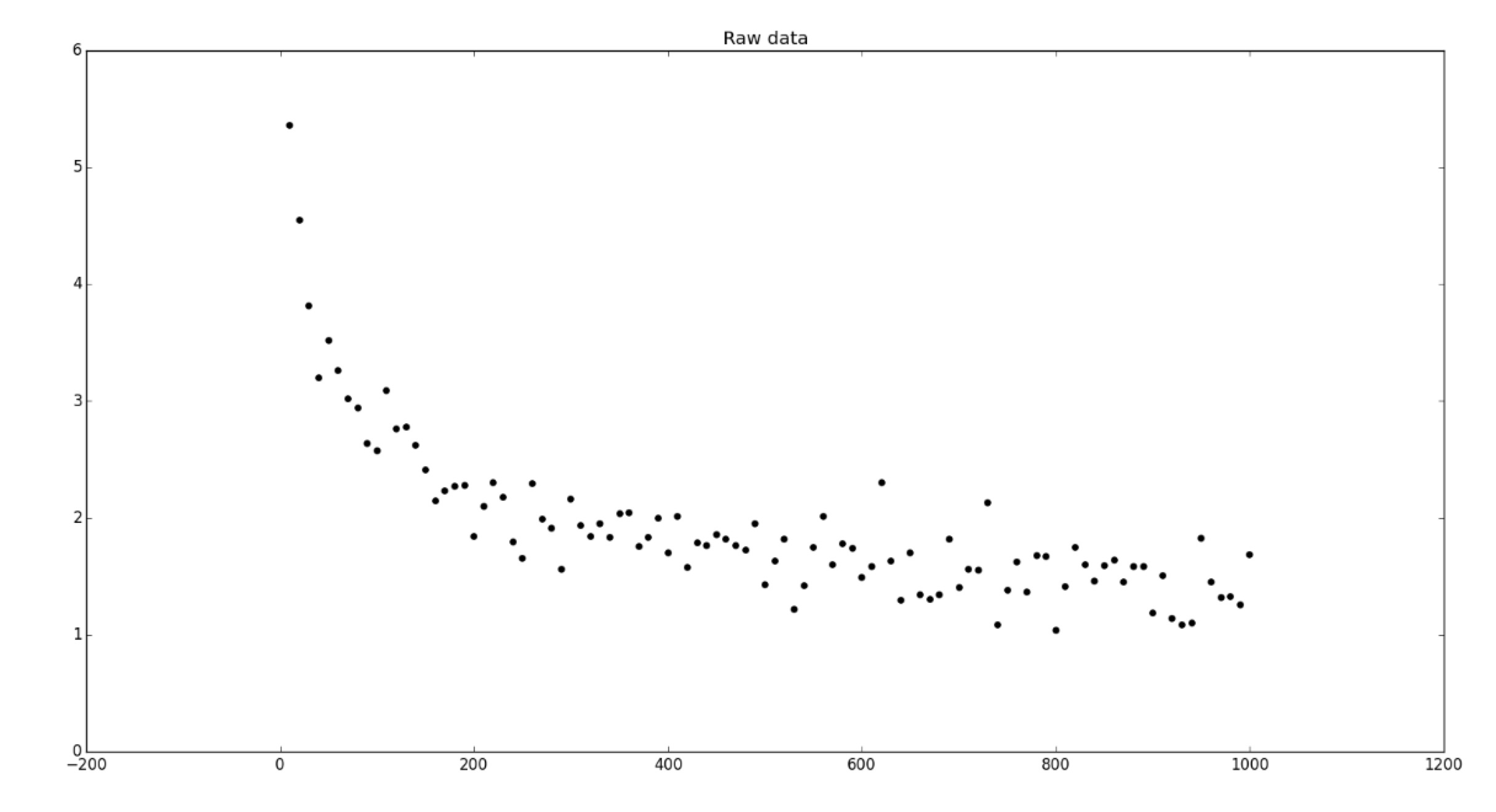
很可能会得到以下曲线：

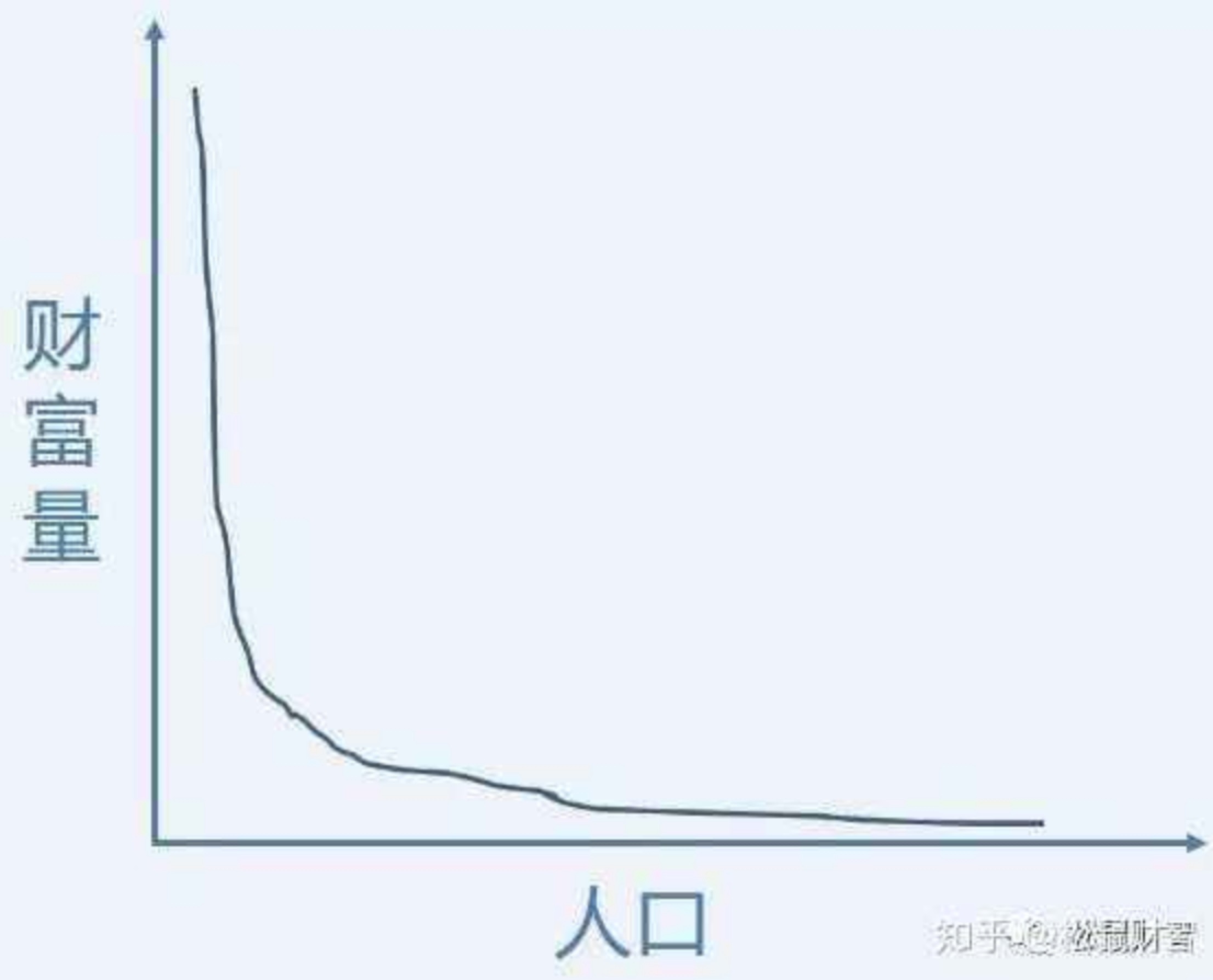
其数学表达式一般如下:

具体推导可参考：

https://blog.csdn.net/dog250/article/details/79146511

IV算法

在机器学习的二分类问题中，IV值（Information Value）主要用来对输入变量进行编码和预测能力评估。特征变量IV值的大小即表示该变量预测能力的强弱。

比如我们有200个候选自变量，通常情况下，不会直接把200个变量直接放到模型中去进行拟合训练，而是会用一些方法，从这200个自变量中挑选一些出来，放进模型，形成入模变量列表。

挑选入模变量过需要考虑的因素很多，比如：变量的预测能力，变量之间的相关性，变量的简单性（容易生成和使用），变量的强壮性（不容易被绕过），变量在业务上的可解释性（被挑战时可以解释的通）等。但是，其中最主要和最直接的衡量标准是变量的预测能力。IV就是这样一种指标，他可以用来衡量自变量的预测能力。类似的指标还有信息增益、基尼系数等等。

比如：我们假设在一个分类问题中，目标变量的类别有两类：Y1，Y2。对于一个待预测的个体A，要判断A属于Y1还是Y2，我们是需要一定的信息的，假设这个信息总量是I，而这些所需要的信息，就蕴含在所有的自变量C1，C2，C3，……，Cn中，那么，对于其中的一个变量Ci来说，其蕴含的信息越多，那么它对于判断A属于Y1还是Y2的贡献就越大，Ci的信息价值就越大，Ci的IV就越大，它就越应该进入到入模变量列表中。

IV值的计算是以WOE为基础的，计算公式如下：

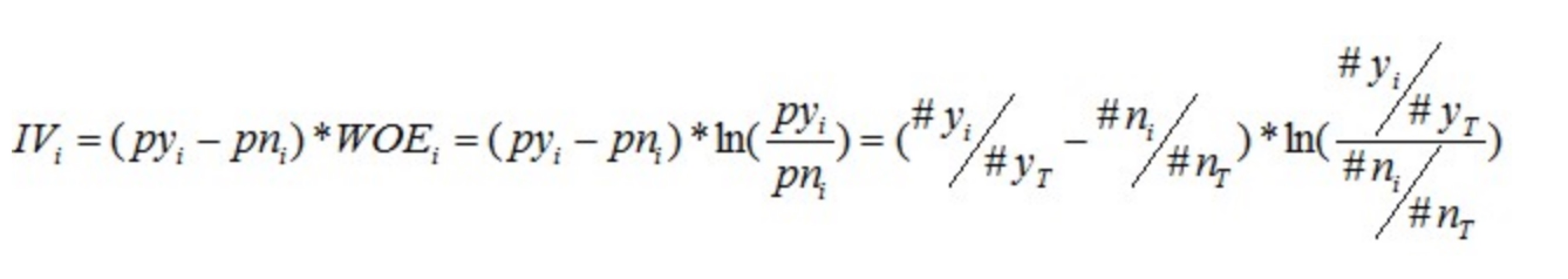
其中WOE（Weight of Evidence，即权重）的计算公式如下：

具体demo可参考：

https://blog.csdn.net/shenxiaoming77/article/details/78771698

参考：

https://blog.csdn.net/dog250/article/details/79146511 https://www.jianshu.com/p/cc4724a373f8 https://blog.csdn.net/shenxiaoming77/article/details/78771698